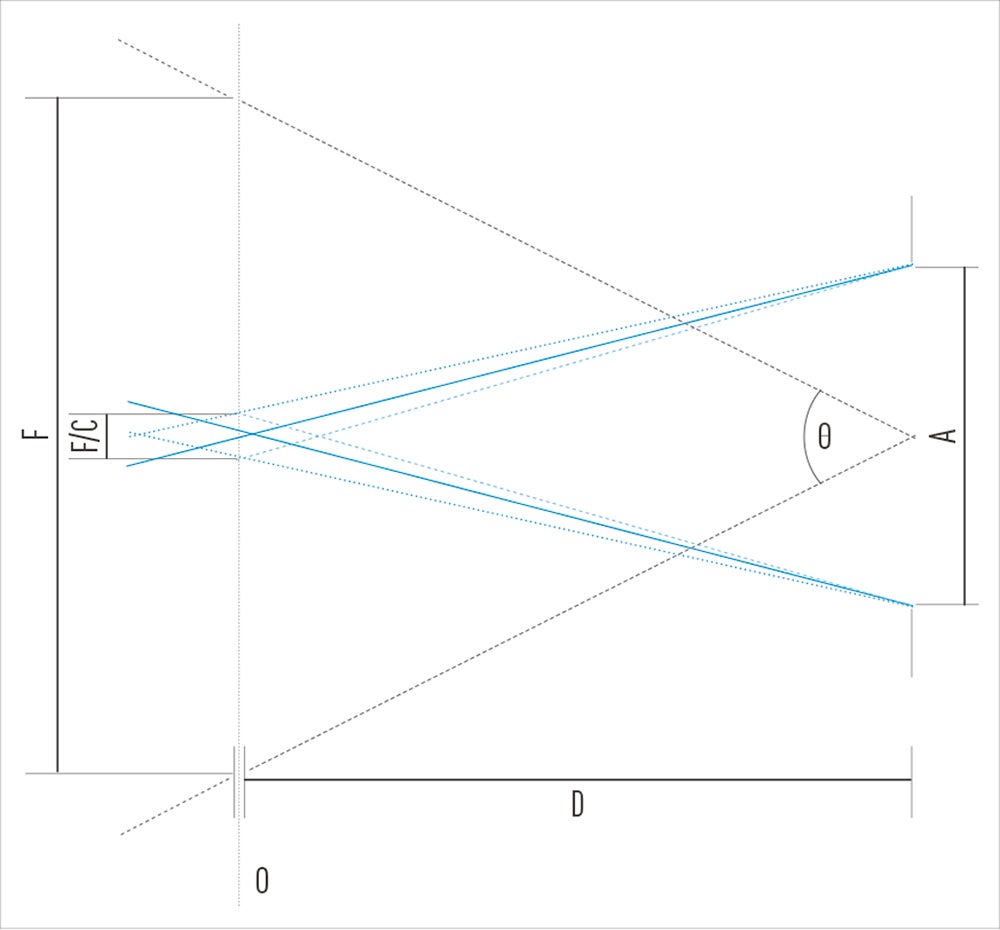
Objects slightly behind or in front of the plane of focus, as indicated by the dotted and dashed blue lines, will be acceptably sharp in print

This article is the first of a series of three in which I’ll try to develop some common elements of photographic theory considering only that which occurs in front of the lens. The motivation for this is to try to remove much of the technical detail, which often provides dead ends when thinking about the basic photographic principles. In the diagram the lens aperture or entrance pupil is shown to the right, with diameter A. Emerging from it is the angle of view that is being captured, denoted by θ. In reality this will be determined by the sensor frame size and the focal length of the lens, but since that happens ‘behind’ the lens, for this discussion how the angle is affected is irrelevant. For this discussion about depth of field (DoF) we add the blue lines, showing the path of light rays to the extremes of the aperture from an object at O, on which we assume the lens is focused. The blue dashed lines show how the rays from an object in front of the plane of focus (denoted by the fine dotted black line) have the appearance of a disc at the plane of focus. Similarly, the blue dotted lines illustrate that the rays from an object behind the plane of focus form a similar disc.

For the purposes of determining DoF, we need to first decide how large a disc we wish to allow as a ‘point’. Normal DoF theory calls this the ‘circle of confusion’, but its position is at the image plane, not the plane of focus. Following Harold Merklinger’s (of The Ins and Outs of Focus fame) lead, I will call its conjugate at the plane of focus the ‘disc of confusion’. The most this disc is relative to the field of view – that is, how large it will appear in the final image. Typically, the circle of confusion is sized to be about 1/1,500th of the image diagonal, so we might choose the disc of confusion to be a similar proportion of the field of view.

The advantage of this way of going about DoF is that it is no longer necessary to choose a circle of confusion appropriate to sensor size and intended viewing size – instead ,we simply choose, as a proportion of the final image, what we will consider to be sharp enough. Further, it dispels the mistaken view that DoF is to do with what happens behind the lens and makes it completely format independent. All that is necessary is to know the angle of view and the aperture diameter.

For the more technically inclined, we can now derive the DoF equations using this ‘in front of camera’ perspective. Using the usual distant object approximations and the laws of similar triangles, we can derive the following:

For a point of focus at distance D from the aperture and a disc of confusion which is a fraction of the field of view C, then the extent of DoF in front of the plane of focus is D/ (CA/2tanθ +1) while the extent behind is D/ (CA/2tanθ -1). While I’m not expecting people to replace the traditional DoF formula with these, it is interesting that they can be derived with no reference to what occurs behind the aperture, so in this form the DoF is format independent. All that is required is to decide what proportion of the field of view is allowable as a ‘disc of confusion’.

Bob Newman is currently Professor of Computer Science at the University of Wolverhampton. He has been working with the design and development of high-technology equipment for 35 years and two of his products have won innovation awards. Bob is also a camera nut and a keen amateur photographer.