Almost two years ago I had a go at explaining F-stop numbers but on re-reading that article Iu2019m not sure how useful it was (and its over-simplification was sometimes so crude as to be inaccurate) so Iu2019m going to tackle F-stop numbers again nowu2026
A couple of months ago What Digital Camera published a comment from a reader pointing out the potential confusion that can exist when F-stop f/22 is referred to as being a “smaller” aperture than F-stop f/16 when in fact the number used (22) is clearly larger (than 16). To understand why 22 truly is smaller in this case it is necessary understand what these numbers measure.
F-stop numbers are actually ratios… they are the result of dividing the focal-length of the lens by the diameter of the lens aperture.
F-stop = (Lens Focal-Length) / (Lens Diameter)
What this means is that if lenses with different focal lengths are to have the same range of F-stop numbers then they need to have different diameter elements. If a 100mm lens and a 50mm lens both offer the same maximum aperture then it means the ratio of focal-length-divided-by-diameter is the same, which in turn means the 100mm lens needs to have elements that are twice the diameter of those used in the 50mm lens. And that is why longer focal-length lenses tend to have larger front elements… because they are trying to deliver similar aperture ranges to those offered by shorter focal-length lenses.
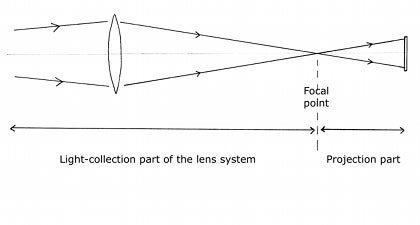
But where does this ratio come from? To answer that question it is best to think about a simple lens that collects light and projects an image onto a waiting camera sensor (as shown in the diagram above). It is fairly obvious that larger lens elements can collect more light. (That is why the human eye’s pupil dilates in low-light conditions… to capture more light.) Less obvious is the fact that doubling the lens diameter quadruples the amount of light collected – because the area of a circle increases with the square of the circle’s diameter so when the diameter doubles the area goes up by two-squared, which is four times.
It is well known that when an image is projected, the brightness of the image falls off with the square of the distance… a behaviour that is known as The Inverse-Square Law. In a simple lens that is imaging a very distant object (located at “infinity”) the projection distance is equal to the focal length of the lens, and clearly this means the brightness of the image that is projected onto the camera sensor will be dimmer for lenses with a longer focal-length.
It would be VERY confusing if exposure settings varied with the focal length of the lens used, so to provide uniform projection brightness under known conditions, independent of the lens focal length, it is necessary to devise a scale in which something else varies to compensate for the longer projection distance in longer focal-length lenses. The “something” chosen is the diameter of the lens. And when the focal-length doubles the diameter of the lens is also doubled to keep the projected brightness the same (because both of those linear measurements actually produce a “squared” effect… one in terms of collecting the light and the other in terms of projecting it).
As for why 22 is actually smaller than 16… the answer is that the diameters are actual lens apertures expressed in fractions of the lens focal length. So “f/22” actually means a lens diameter that is equal to 1/22nd of the lens focal length. Similarly, “f/16” means a lens diameter that measures 1/16th of the lens focal length. The fact that these numbers are often written simply as 22 and 16 is nothing more than shorthand… and although 22 is a bigger number than 16, 1/22 is clearly a smaller fraction than 1/16.